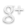-
-
1.2- les principaux types d’engrenages
1.2.1- Les engrenages cylindriques à denture droite
Avantages : – Simple et économique
- Pas d’efforts axiaux
- Inconvénients :
- Vitesses de rotation limitées
- Bruyant
- Entraxes prenant des valeurs finies

Pignon baladeur droit avec entrée de dent cannelé intérieur en acier trempé
1.2.2- Les engrenages cylindriques à denture hélicoïdale
Avantages :
- Transmission plus souple et moins bruyante
- Transmission d’efforts et de vitesses plus importants
- Possibilités d’entraxes infinis
-
Inconvénients :
Effort axial supplémentaire
-
-
- Solution moins économique
- Rendement moins bon

Engrenage hélicoïdale cannelé long pour machine outils
Fabrication de pignons + engrenages :taillage d’engrenage1.2.3- Les engrenages coniques
Avantages :
- Arbres non parallèles voir non concourants
- Possibilité de choisir le sens de rotation de la roue menée Inconvénients :
- Solution moins économique
- Nécessité d’un réglage des roues au montage
-

Pignon conique réalisé sur tailleuse à couteaux
1.2.4- Les engrenages à roue et vis sans fin
Avantages : – Arbres quelconques (Très souvent orthogonaux)
- Rapport de réduction élevés Inconvénients : – Rendement faible
- Parfois non réversible (peut être un avantage)

Roue à vis bronze UE12 De 800 61 dents module 11 + vis sans fin module 11 2 entrées pour arcellormittal
1.3- Cinématique d’un engrenage
On pose :
Quelque soit le type d’engrenage, on peut définir les rapports de :
Transmission : rréduc =
Réduction : rtrans =
Nmenante : Fréquence de rotation de la roue menante
Nmenée : Fréquence de rotation de la roue menée
Zmenante : Nombre de dents de la roue menante (Nombre de filets de la vis pour l’engrenage à roue et vis sans fin)
Zmenée : Nombre de dents de la roue menée
2. Engrenages cylindriques à denture droite
2.1- Paramètres d’un engrenage
Ce type d’engrenage peut-être de deux types : les engrenages extérieurs (pignon roue) ou intérieur (pignon couronne).
Chaque roue, pignon ou couronne est définie par :
- Son nombre de dents : Z
- Sa largeur : b
- Par contre sont commun aux deux roues de l’engrenage :
- Le module des dents : m
- L’angle de pression : α
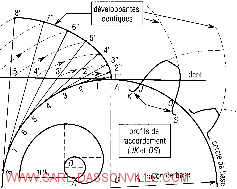
2.2- Eléments d’un engrenage
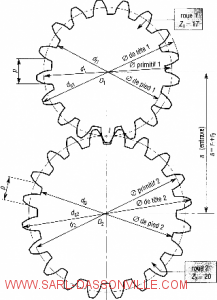
Pour un engrenage, on définit :
-
Cercles ou cylindres primitifs : Ce sont des cercles représentants deux roues de friction ayant le même rapport de transmission. (Ces cercles sont tangents).
-
Cercles ou cylindres de tête : Ce sont des cercles passant par les sommets des dents.
-
Cercles ou cylindres de pied : Ce sont des cercles passant par les pieds des dents.
-
Entraxe : C’est la distance entre les deux axes des deux roues.
-
Pas primitif : C’est la distance entre deux dents consécutives au niveau du cercle primitif.
-
Droite d’action : C’est la droite normale au contact entre les dents des deus roues. Elle est donc le support de l’action d’une roue sur l’autre.
-
Angle de pression : La droite d’action est invariante quelque soit la position des roues. Elle est inclinée d’un angle α appelé angle de pression par rapport à la tangente aux cercles primitifs
-
Saillie et creux d’une dents : Ce sont les parties de la dent se situant entre le cercle primitif et respectivement le cercle tête et le cercle de pied de l’engrenage.
- Profil en développante de cercle : C’est le profil des dents d’un engrenage. Il est obtenu en faisant rouler sans glisser une droite sur un cercle appelé cercle de base défini par son diamètre : Db = D*cos α (Où D est le diamètre primitif de la roue ). Ce profil permet de réduire au mieux le glissement entre les dent d’un engrenage
-
-
3.2- Dimensionnement de la roue
Le dimensionnement de la roue est en grande partie identique à celui d’une roue d’engrenage cylindrique à denture hélicoïdale :
Diamètre primitif de la roue : DR =
3.3- Dimensionnement de la vis
3.3.1- Relation entre la vis et la roue
Pour permettre un engrènement correct de la vis et de la roue, les paramètres de la vis sont liés à ceux de la roue par les deux relation suivante :
- Relation entre les deux angles d’hélice :
- Relation entre les pas de la vis et de la roue :
Où : Pt est le pas apparent de la roue
et PX est la pas axial de la vis (Distance entre deux profils consécutifs)
3.3.2- Dimensions de la vis
Pas hélicoïdal de la vis (distance entre deux profils d’un même filet) :
PZ = Diamètre primitif de la vis : PZ = ZV.PX
DV = Diamètre primitif de la vis
3.4- Entraxe
L’entraxe correspond à la distance minimale entre le centre de chaque roue dentée de l’engrenage.
a = (d1 + d2 )/2 = (Z1 + Z2)*m/2
Dans le cas de roue vis sans fin
a=(dV + dR)
Familiarisation avec un engrenage
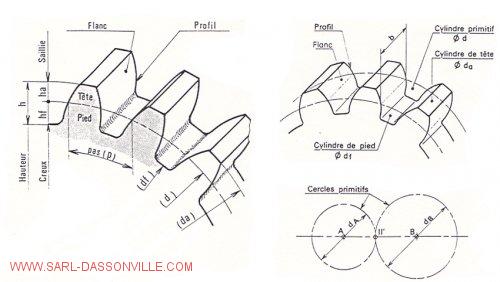
– Øda : cylindre de tête => da = d + 2m
– Ødf : cylindre de pied => df = d – 2.5m
– b : largeur de denture
– h : hauteur de denture => ha + hf = 2.25m
– ha : saillie => ha = m
– hf : creux => hf = 1.25m
– Z : nombre de dents
– p : pas => p = m * π
– m : module
– Ød : cylindre primitif
Le module est un rapport m = p / π , il est déterminé par le calcul de résistance des matériaux.
Toutes roues de même module s’engrenent entre-elles.
Les modules normalisés
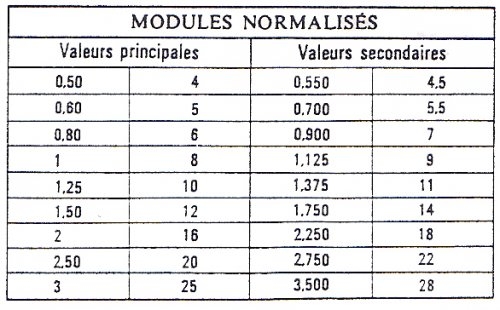
Voir nos services en : taillage d’engrenage
Sens de rotation
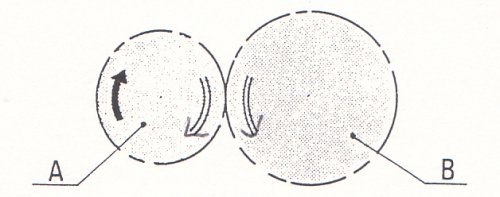
La roue B ne tourne pas dans le même sens que la roue A.
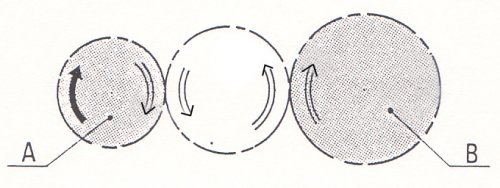
La roue B tourne dans le même sens que la roue A.
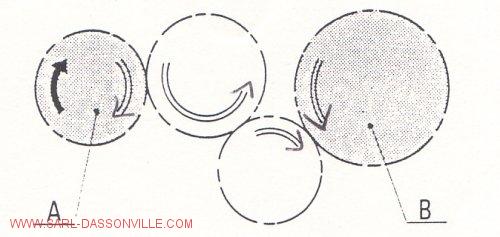
La roue B ne tourne pas dans le même sens que la roue A.
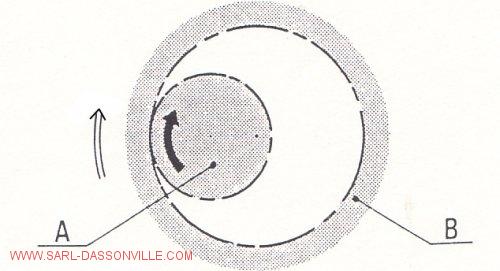
La roue B tourne dans le même sens que la roue A.